| ■43■ 円に内接する正三角形の重心と放射線 The center of the equilateral triangle and radiation |
|
<円に内接する正三角形とプロニティー>
pronity45/30/90=A/B/C pronity45/30/18=A/B/D |
|
プロニティー関係にある4つの円に内接する正三角形 正三角形Aの中心と正三角形Bの頂点を結ぶ交点が正三角形Dの3つの頂点、正三角形Bの中心と正三角形Aの頂点を結ぶ線の交点がもう一つの逆正三角形Dとなる。 点a1は時計回りに60度づつ回転したB.C上のb3.c2の座標を結ぶ線と、反時計回りに60度回転したB.C上の座標b1.c3を結ぶ線の2本の直線の関係にあり、 正三角形の他の2つの頂点も、同様の関係を持ち、このことから正三角形A.Bの頂点から正三角形Cの頂点を求める事が出来る。 |
| ▼正三角形A.Bから求めた正三角形C.D |
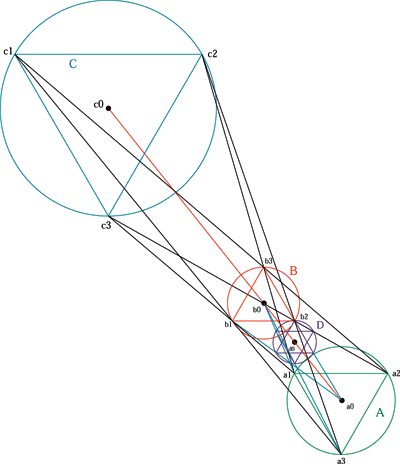
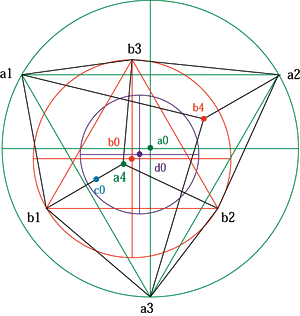
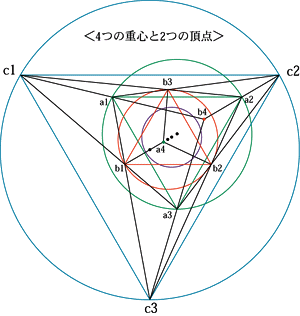
<2つの円A.Bが離れた場合と重なった場合> <4つの重心と2つの頂点>
pronity45/30/90/18=pronityA/B/C/D Cの中心 Dの中心
|
|
 |
*PDF書類では図形を拡大して鮮明に見ることが出来ます
Copyright (C) 2010 Masaki Matsuura. All rights reserved.

dream & harmony


