
相対するモノとモノから導かれるもう一つのモノあるいは相対するモノとモノに干渉するもう一つのモノ |
3つの正三角形に見るプロニティ 正三角形ABの頂点を結ぶ線を延長すると3つの消点Cで交わり、この3 つの点c1.c2.c3を結んでできる正三角形Cは正三角形AとBと共にプロニティの関係を持つ3つの正三角形となります |
 |
A.Bに相対する正三角形Cの値は A.Bの積をA.Bの差で割る事で求められる |
3次元立体を描くための3つの消点となる正三角形C この3つの消点c1.c2.c3と正三角形A.Bの頂点を結ぶ放射線は正三角形A.Bを対角線とする立方体の12本の稜線を形成します。 |
 |
立方体の手前の頂点a4は 3つの消点Cと正三角形Aの頂点を結んで得られる |
2つの物体の相対する座標を結んだ時に現れるもう1つの物体 点C1.2.3を結んでできる正三角形Cの値はC=A×B÷(A-B)で求められる。こうして求められる3つの三角形の関係をプロニティ(三位一体の比例)と呼び、この関係は線分、円、球の関係においても同等である。 |
 |
この3 つの消点Cを形成する三角形Cと それを導きだした三角形ABとの3つの三角形の関係がプロニティです。 |
![]()
正三角形Cの3頂点は 正三角形ABに対する3次元の消点でもあります。 |
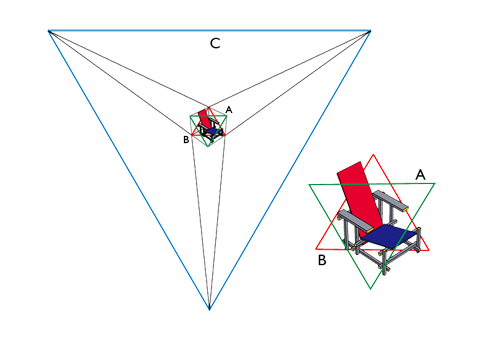
プロニティA・B・Cの関係から描かれたリートフェルトの椅子の透視図 |
発案:松浦正樹 Masaki Matsuura
デザイン:バースデザイン研究所
Copyright (C) 2010 Masaki Matsuura. All rights reserved.

dream & harmony
![]()